[자료구조] Graph - 그래프 개념, 인접행렬, 인접리스트 구현

자료구조 07 - 1 / Graph

---

정의 

https://www.raywenderlich.com

각 객체(꼭지점, 정점: vertex, vertices, Node)가 간선(Edge, Link)으로 서로 이어져 있는 집합, 사이클(순환)을 허용한다.

 

E(u, v) = souce vertex에서 destination vertex로 가는 edge

Degree 각 정점에 연결된 Edge 수 (Directed Graph에서 나가는 간선 개수 Outdegree/ 들어오는 간선 개수 Indegree 

weighted Graph 가중 그래프

Sub Graph 부분 그래프

완전 그래프 (모든 정점 간선으로 연결

 

Weighted Graph

 

Directed Graph(Digraph) and Undirected Graph

 

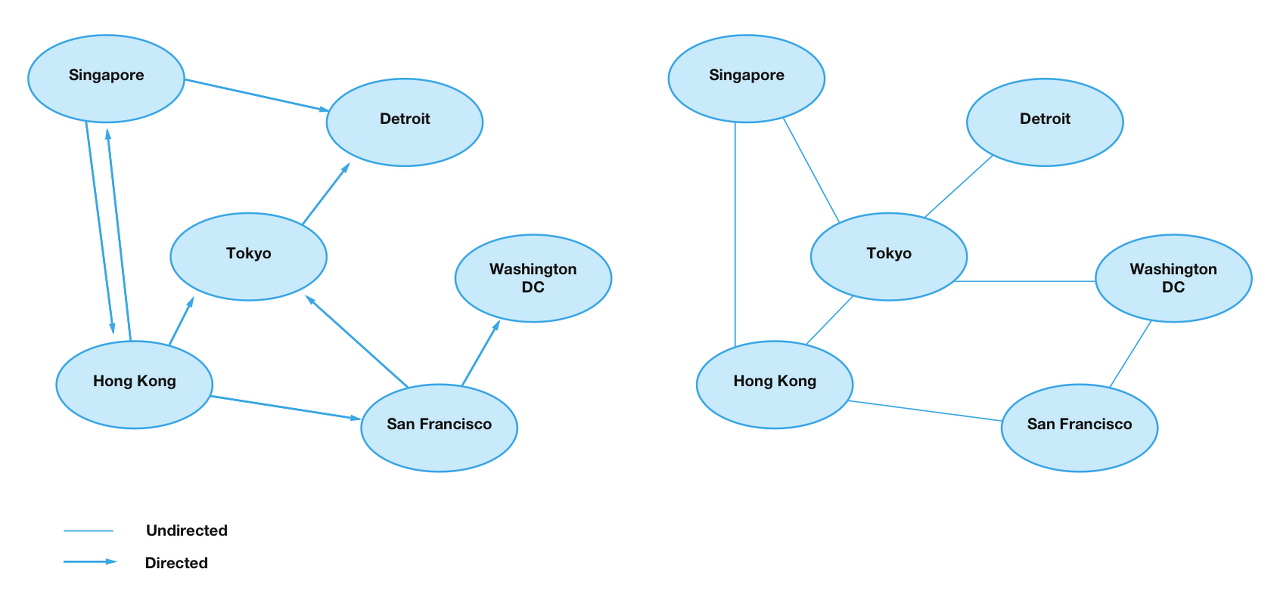
Representing a Graph

 

Approch 접근방식

Storing an array of Arrays: 행렬 저장방식 (이차원 배열)

 

- index (source, destination)와 value는 간선의 갯수 파악 O(1), 탐색 속도 비교적 빠름, 간선 확인 비교적 빠름

 

 

Storing an array of Linked-lists: 연결 리스트 저장방식

 

- index는 edge, value는 vertex, 빠른 삽입/삭제 시간이 필요한 경우, 정점간 연결 확인이 오래 걸림, 탐색 O(n) 간선 갯수, 공간 낭비 적음, 구현 복잡

Storing a Dictionary of arrays: 딕셔너리 저장방식

- 각 객체를 만들고 딕셔너리의 Items로 사용 key가 edge, value는 vertex  

 

 

활용

지하철 노선, 도록, 소셜 네트워크, 신경망, 금융등

사물간의 순서 를 그래프로 표현, 관계를 표현

 

네비게이션 길막힘?! (공사중)

 

구현

 

 

Implementing the Adjacency List & Matrix

public struct Edge<T>: Equatable where T: Equatable, T: Hashable {

  public let from: Vertex<T>
  public let to: Vertex<T>

  public let weight: Double?

}
public struct Vertex<T>: Equatable where T: Equatable, T: Hashable {

  public var data: T
  public let index: Int

}

private class EdgeList<T> where T: Equatable, T: Hashable {

  var vertex: Vertex<T>
  var edges: [Edge<T>]? = nil

  init(vertex: Vertex<T>) {
    self.vertex = vertex
  }

  func addEdge(_ edge: Edge<T>) {
    edges?.append(edge)
  }
  func createVertex(_ data: T) -> Vertex<T> {
  	// 방식별로
  }
}

// 인접 리스트
open override func createVertex(_ data: T) -> Vertex<T> {
   // check if the vertex already exists
   let matchingVertices = vertices.filter() { vertex in
      return vertex.data == data
   }

   if matchingVertices.count > 0 {
      return matchingVertices.last!
   }

   // if the vertex doesn't exist, create a new one
   let vertex = Vertex(data: data, index: adjacencyList.count)
   adjacencyList.append(EdgeList(vertex: vertex))
   return vertex
}
// v1 -> [(v2: 1.0)]
// v2 -> [(v3: 1.0), (v5: 3.2)]
// v3 -> [(v4: 4.5)]
// v4 -> [(v1: 2.8)]

// 인접 행렬
open override func createVertex(_ data: T) -> Vertex<T> {
  // check if the vertex already exists
  let matchingVertices = vertices.filter() { vertex in
    return vertex.data == data
  }

  if matchingVertices.count > 0 {
    return matchingVertices.last!
  }

  // if the vertex doesn't exist, create a new one
  let vertex = Vertex(data: data, index: adjacencyMatrix.count)

  // Expand each existing row to the right one column.
  for i in 0 ..< adjacencyMatrix.count {
    adjacencyMatrix[i].append(nil)
  }

  // Add one new row at the bottom.
  let newRow = [Double?](repeating: nil, count: adjacencyMatrix.count + 1)
  adjacencyMatrix.append(newRow)

  _vertices.append(vertex)

  return vertex
}
// [[nil, 1.0, nil, nil, nil]    v1
//  [nil, nil, 1.0, nil, 3.2]    v2 
//  [nil, nil, nil, 4.5, nil]    v3
//  [2.8, nil, nil, nil, nil]    v4
//  [nil, nil, nil, nil, nil]]   v5
//
//   v1   v2   v3   v4   v5

Implementing The Dictionary of the Adjacency List: 딕셔너리

Vertices

 

// Swift 5
// raywenderlich.com

public struct Vertex<T: Hashable> {
  var data: T
}
extension Vertex: Hashable {
  public var hashValue: Int { // 1
      return "\(data)".hashValue
  }
  
  static public func ==(lhs: Vertex, rhs: Vertex) -> Bool { // 2
    return lhs.data == rhs.data
  }
}
extension Vertex: CustomStringConvertible {
  public var description: String {
    return "\(data)"
  }
}

Edges

public enum EdgeType {
  case directed, undirected
}
public struct Edge<T: Hashable> {
  public var source: Vertex<T> 	// 간선이 출발하는 정점
  public var destination: Vertex<T>
  public let weight: Double? 	// 숫자를 이용해서 weight 부여
}
extension Edge: Hashable {
  
  public var hashValue: Int {
      return "\(source)\(destination)\(weight)".hashValue
  }
  
  static public func ==(lhs: Edge<T>, rhs: Edge<T>) -> Bool {
    return lhs.source == rhs.source &&
      lhs.destination == rhs.destination &&
      lhs.weight == rhs.weight
  }
}

Graphable Protocol

protocol Graphable {
  associatedtype Element: Hashable 						// Generic 타입 선택	
  var description: CustomStringConvertible { get } 		// 검산용 프린트
  
  func createVertex(data: Element) -> Vertex<Element> 	// 정점 생성
  
  func add(_ type: EdgeType, from source: Vertex<Element>, 
   to destination: Vertex<Element>, weight: Double?) 	
  // Edge 타입을 구분해서 정점사이에 Edge 추가
  
  func weight(from source: Vertex<Element>, 
  		   to destination: Vertex<Element>) -> Double? 	
  // 두 정점 사이 weight 반환 
  
  func edges(from source: Vertex<Element>) -> [Edge<Element>]? 
  // source 정점의 edge 반환
}

Adjacency List

open class AdjacencyList<T: Hashable> {
  public var adjacencyDict : [Vertex<T>: [Edge<T>]] = [:]
  public init() {}
}
extension AdjacencyList: Graphable {
  public typealias Element = T
  
  public func createVertex(data: Element) -> Vertex<Element> {
  	let vertex = Vertex(data: data)
  
  	if adjacencyDict[vertex] == nil {
       adjacencyDict[vertex] = []
  	}

    return vertex
  }
}

extension AjacencyList {
   public func add(_ type: EdgeType, from source: Vertex<Element>, 
   		   to destination: Vertex<Element>, weight: Double?) {
     switch type {
     case .directed:
        addDirectedEdge(from: source, to: destination, weight: weight)
     case .undirected:
        addUndirectedEdge(vertices: (source, destination), weight: weight)
     }
   }
   fileprivate func addDirectedEdge(from source: Vertex<Element>, 
   		to destination: Vertex<Element>, weight: Double?) {
     let edge = Edge(source: source, destination: destination, weight: weight) // Edge 생성
     adjacencyDict[source]?.append(edge) // Edge를 souce 정점에 연결 
   }
   fileprivate func addUndirectedEdge(vertices: (Vertex<Element>, Vertex<Element>), 
    									 weight: Double?) {
     let (source, destination) = vertices
     addDirectedEdge(from: source, to: destination, weight: weight)
     addDirectedEdge(from: destination, to: source, weight: weight)
   }
}

 

 

extension Ajac
  public func weight(from source: Vertex<Element>, 
  				  to destination: Vertex<Element>) -> Double? {
    guard let edges = adjacencyDict[source] else { 	// source 정점에서 Edge 없으면 
       return nil
    }
    for edge in edges { 					// 각 Edge를 방문 
       if edge.destination == destination { 	// Edge의 목적지 비교를 이용해 해당 Edge의 weight 찾기
         return edge.weight
       }
    }
     return nil 							// weight 없으면
  }
  public var description: CustomStringConvertible {
     var result = ""
     for (vertex, edges) in adjacencyDict {
        var edgeString = ""
        for (index, edge) in edges.enumerated() {
           if index != edges.count - 1 {
           edgeString.append("\(edge.destination), ")
        } else {
           edgeString.append("\(edge.destination)")
        }
      }
      result.append("\(vertex) ---> [ \(edgeString) ] \n ")
      }
    return result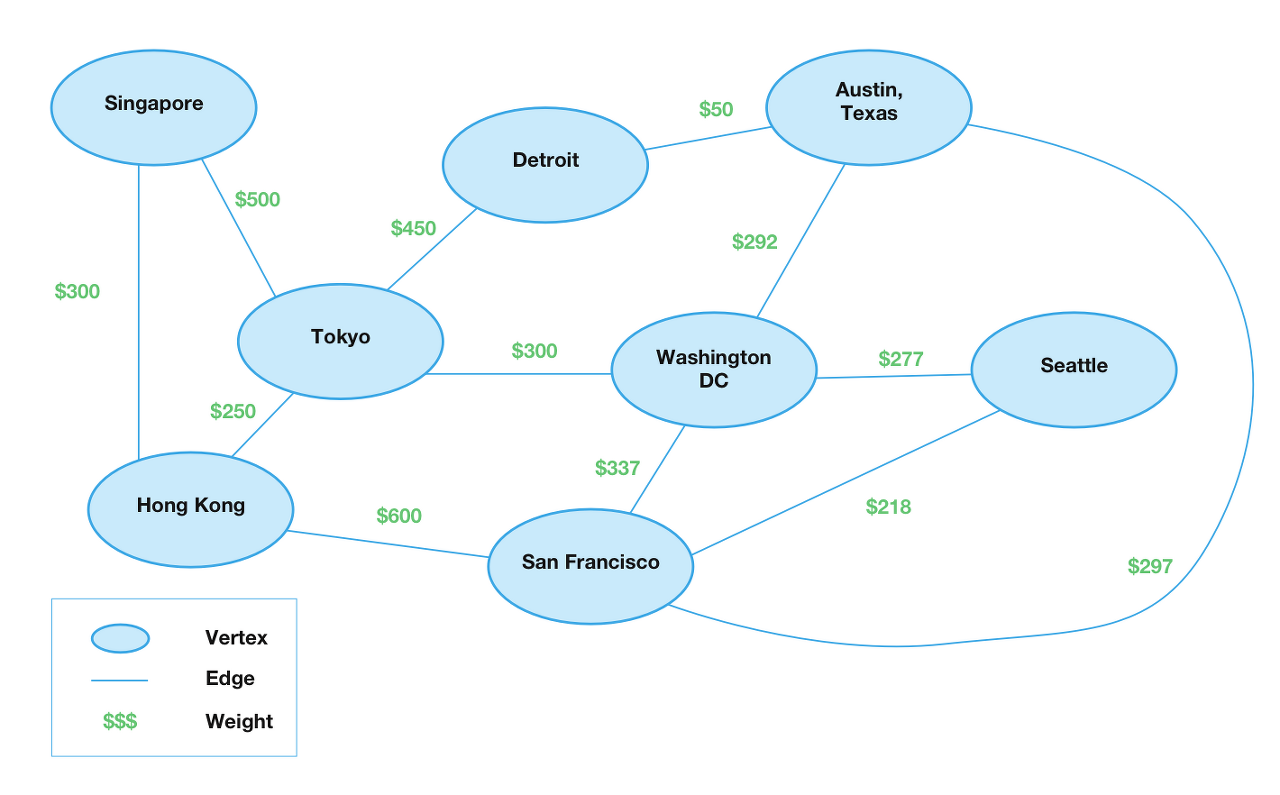
  }
}

 

let adjacencyList = AdjacencyList<String>()

let singapore = adjacencyList.createVertex(data: "Singapore")
let tokyo = adjacencyList.createVertex(data: "Tokyo")
let hongKong = adjacencyList.createVertex(data: "Hong Kong")
let detroit = adjacencyList.createVertex(data: "Detroit")
let sanFrancisco = adjacencyList.createVertex(data: "San Francisco")
let washingtonDC = adjacencyList.createVertex(data: "Washington DC")
let austinTexas = adjacencyList.createVertex(data: "Austin Texas")
let seattle = adjacencyList.createVertex(data: "Seattle")

adjacencyList.add(.undirected, from: singapore, to: hongKong, weight: 300)
adjacencyList.add(.undirected, from: singapore, to: tokyo, weight: 500)
adjacencyList.add(.undirected, from: hongKong, to: tokyo, weight: 250)
adjacencyList.add(.undirected, from: tokyo, to: detroit, weight: 450)
adjacencyList.add(.undirected, from: tokyo, to: washingtonDC, weight: 300)
adjacencyList.add(.undirected, from: hongKong, to: sanFrancisco, weight: 600)
adjacencyList.add(.undirected, from: detroit, to: austinTexas, weight: 50)
adjacencyList.add(.undirected, from: austinTexas, to: washingtonDC, weight: 292)
adjacencyList.add(.undirected, from: sanFrancisco, to: washingtonDC, weight: 337)
adjacencyList.add(.undirected, from: washingtonDC, to: seattle, weight: 277)
adjacencyList.add(.undirected, from: sanFrancisco, to: seattle, weight: 218)
adjacencyList.add(.undirected, from: austinTexas, to: sanFrancisco, weight: 297)

print(adjacencyList.description)

추가적으로 생각해볼 내용

면접 예상질문

Q: 트리도 노드와 간선으로 이루어져 있는데 차이점은?

A: 그래프는 트리와 달리 root(시작점) 개념이 없으며 노드간의 관계에서 부모, 자식 관계를 가지지 않음, indirect와 direct 두가지를 선택적으로 가능(트리는 directed graph), 트리와 달리 Cycle(순환)이 가능함

 

Reference : raywenderlich.com github explain