[자료구조] Tree - Binary Search Tree

자료구조 05 - 3 / Tree - BinarySearchTree (BST)

---

정의 

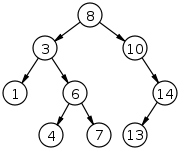
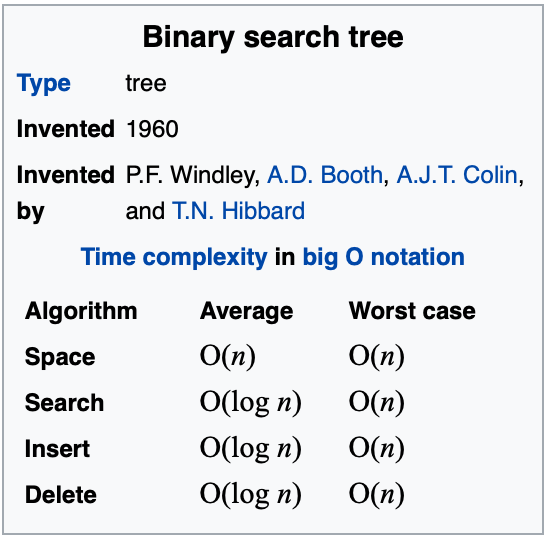
이진 탐색트리 예시 (left < root < right) / 탐색 예시 (4) / 이진 탐색트리 시간복잡도 관련

이진트리의 종류 중 하나로 Ordered or Sorted Binary Tree로 불림

이진트리로 Subtree가 추가 될때 조건을 가짐, 예를 들어 Current Node 보다 작으면 Left, 크면 Right Child로 추가됨

저장 규칙 (조건)이 좀 더 효율적인 트리로 만들어줌

 

일반적인 이진트리보다 빠른 탐색 속도를 가진다. 

 

추가 Inserting

추가될 노드의 부모노드가 될때까지의 높이(h)를 거치며 조건에 맞게 자리 잡으므로 O(h) time 소요

탐색 Searching

마찬가지로 추가될 노드의 값을 조건을 확인하며 찾아가므로O(h) time 소요

순회 Traversing

In-Order : left -> root -> right

Pre-Order : root -> left -> right

Post-Order : left -> right -> root

 

 

 

 

 

삭제 Deleting

Leaf Node 삭제

 

삭제할 노드가 Leaf Node 인 경우 참조 해제만 해주면 됨

 

Leaf Node 가 아닌경우

Leaf Node 가 아닌 삭제 (root)

삭제 하려는 노드의 Left SubTree의 가장 큰 수 노드 또는 Right SubTree의 가장 작은 수 노드 중 하나로 대체 

 

구현

기본 구현

// Swift 5
// Referenced by raywenderlich.com

class BinarySearchTree<T: Comparable > {
    var value: T
    var parent: BinarySearchTree?
    var leftChild: BinarySearchTree?
    var rightChild: BinarySearchTree?
    
    init(value: T) {
        self.value = value
    }
    
    var isRoot: Bool {
        return parent == nil
    }
    
    var isLeaf: Bool {
        return leftChild == nil && rightChild == nil
    }
    
    var hasBothChildren: Bool {
        return leftChild != nil && rightChild != nil
    }
    
    var isLeftChild: Bool {
        return parent?.leftChild === self
    }

    var count: Int {
        return (leftChild?.count ?? 0) + 1 + (rightChild?.count ?? 0)
    }
}

 

추가 Inserting

extension BinarySearchTree {	// Inserting
    func insert(value: T) {
        if value < self.value {
            if let left = leftChild {
                left.insert(value: value)
            } else {
                leftChild = BinarySearchTree(value: value)
                leftChild?.parent = self
            }
        } else {
            if let right = rightChild {
                right.insert(value: value)
            } else {
                rightChild = BinarySearchTree(value: value)
                rightChild?.parent = self
            }
        }
    }
}

탐색 Searching

extension BinarySearchTree {	// Searching
    func search(value: T) -> BinarySearchTree? {
        if value < self.value {
            return leftChild?.search(value: value)
        } else if value > self.value {
            return rightChild?.search(value: value)
        } else {
            return self  // found it!
        }
    }
}

순회 Traversing

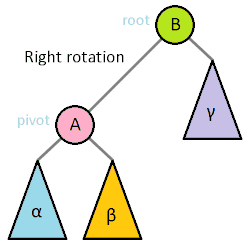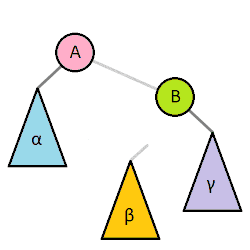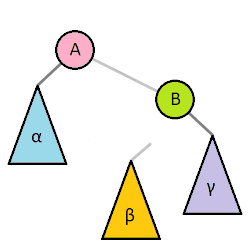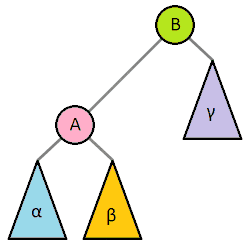
extension BinarySearchTree {	// Travesing
    func inOrder(process: (T) -> Void) {
       leftChild?.inOrder(process: process)
       process(value)
       rightChild?.inOrder(process: process)
     }

    func preOrder(process: (T) -> Void) {
       process(value)
        leftChild?.preOrder(process: process)
        rightChild?.preOrder(process: process)
     }

    func postOrder(process: (T) -> Void) {
        leftChild?.postOrder(process: process)
        rightChild?.postOrder(process: process)
       process(value)
     }
}

삭제 Deleting (Figure 2, Left SubTree's Leaf)

extension BinarySearchTree {	// Deleting
    func minimum() -> BinarySearchTree {
        var node = self
        while let next = node.leftChild {
            node = next
        }
        return node
    }
    
    func maximum() -> BinarySearchTree {
        var node = self
        while let next = node.rightChild {
            node = next
        }
        return node
    }
    
    func removeNode(value: T) {
        if let toRemoveNode = self.search(value: value) {
            removeNode(node: toRemoveNode)
        } else {
            print("There isn't value \(value) Node")
        }
    }
    
    func removeNode(node: BinarySearchTree) {
        if node.isLeaf { // node는 leaf node
            removeLeaf(node: node)
        } else {
            var toReplaceNode: BinarySearchTree? = nil
            
            if node.leftChild!.isLeaf { // 삭제할 노드의 leftChild로 대체될 경우
                toReplaceNode = node.leftChild
            } else {    // 삭제할 노드의 leftChild의 Maximum으로 대체. 될 경우
                toReplaceNode = node.leftChild?.maximum()
                
                if toReplaceNode!.isLeaf {
                    toReplaceNode!.parent?.rightChild = nil // 대체할 노드의 부모 노드에서 제거
                } else {    // 대체할 노드의 왼쪽 자식노드 존재
                    toReplaceNode?.parent?.rightChild = toReplaceNode?.leftChild
                    toReplaceNode?.leftChild?.parent = toReplaceNode?.parent
                }
            }
            
            // 삭제된 노드 자리로 대체
            if let parent = node.parent {
                toReplaceNode?.parent = parent
                if node.isLeftChild {
                    parent.leftChild = toReplaceNode
                } else {
                    parent.rightChild = toReplaceNode
                }
            } else {
                node.value = toReplaceNode!.value
            }
            
            if let right = node.rightChild {
                toReplaceNode?.rightChild = right
                right.parent = toReplaceNode
            }
        }
    }
    
    func removeLeaf(node: BinarySearchTree) {
        let parent = node.parent
        
        if parent?.rightChild?.value == node.value {
            parent?.rightChild = nil
        } else if parent?.leftChild?.value == node.value {
            parent?.leftChild = nil
        }
        
        node.parent = nil
    }
}

출력 Description

extension BinarySearchTree: CustomStringConvertible {	// Description
    var description: String {
        var s = ""
        if let left = leftChild {
            s += "(\(left.description)) <- "
        }
        s += "\(value)"
        if let right = rightChild {
            s += " -> (\(right.description))"
        }
        return s
    }
}

높이 Height 및 이진트리 확인 isBST

extension BinarySearchTree {
    func height() -> Int {
        if isLeaf {
            return 0
        } else {
            return 1 + max(leftChild?.height() ?? 0, rightChild?.height() ?? 0)
        }
    }
    
    func isBST(minValue: T, maxValue: T) -> Bool {
        if value < minValue || value > maxValue {
            return false
        }
        let leftBST = leftChild?.isBST(minValue: minValue, maxValue: value) ?? true
        let rightBST = rightChild?.isBST(minValue: value, maxValue: maxValue) ?? true
        
        return leftBST && rightBST
    }
}

추가적으로 생각해볼 내용

최악의 상황 (Worst)

(참조) The shapes of the BST

조건을 따라 추가되었지만 이진트리가 고르지 못하고 한쪽으로 쏠려서 Height (Depth)가 길어진 경우,

Node의 총갯수 N 과 높이 h 가 같아 질수도 있다. O(h)

-> 트리의 균형을 맞추는 AVL Tree 가 제안됨

(참조) AVL Tree Single Rotation

활용사례

검색 엔진 (알파벳, 문자 검색 등) 

 

 

Wikipedia
Interview_Question_github
raywenderlich.com