-
[자료구조] Tree - Binary TreeArchive/CS & App 2021. 5. 3. 23:53728x90
자료구조 05 - 2 / Tree - BinaryTree
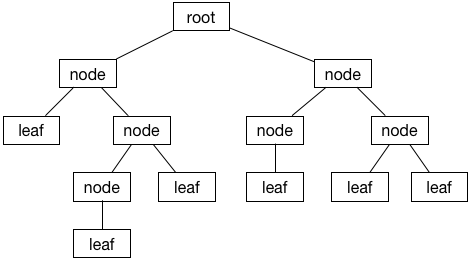
정의
트리 구조에서 2개의 서브트리만 가지는 트리의 형태, 모든 노드의 자식노드는 두개의 서브트리만 가짐
이진트리의 Leaf Node의 상태에 따라서
* (N = level)
Perfect Binary Tree (포화 이진 트리) : 모든 레벨에 노드가 채워진 트리 (총 Node 갯수 : 2ᴺ + 1 개 / Leaf의 갯수: 2ᴺ 개)
Complete Binary Tree (완전 이진 트리) : 자식노드가 왼쪽 -> 오른쪽 형태로 채워진 트리
Full Binary Tree (정 이진 트리) : 자식노드가 없거나 2개인 노드로 채워진 트리
로 구분지어 표현 할수 있다.
구현
class BinaryTreeNode<T: Equatable>: Node<T> { var leftChild: Node<T>? var rightChild: Node<T>? override init(value: T) { super.init(value: value) } override func add(child: BinaryTreeNode<T>) { if leftChild == nil { leftChild = child child.parent = self } else if rightChild == nil { rightChild = child child.parent = self } else { print("This Node has Children") } } override func search(value: T) -> BinaryTreeNode<T>? { if value == self.value { // Equatable return self } if let found = leftChild?.search(value: value) as? BinaryTreeNode<T> { return found } else if let found = rightChild?.search(value: value) as? BinaryTreeNode<T> { return found } return nil } }// Array를 이용한 이진트리 구현 struct BinaryTreeArray { static var tree = [Int?]() static func parent(current: Int) -> Int? { return current > 0 ? (current - 1) / 2 : nil } static func first(current: Int) -> Int? { return current*2+1 > tree.count ? nil : current*2+1 } static func second(current: Int) -> Int? { return (current+1)*2 > tree.count ? nil : (current+1)*2 } } BinaryTreeArray.tree = [0, 1, 2, 3, 4, 5, 6, 7] print(" 3's parent \(BinaryTreeArray.parent(current: 3)!)") print(" root's right child \(BinaryTreeArray.second(current: 0)!)")추가적으로 생각해볼 내용
노드 추가 및 제거 프로세스


노드 추가 / 노드 삭제 프로세스 
순회 (Traversal) ( 1+2 )
전위 순회 (Pre-order Traverse) : Root -> Left -> Right 순서 방문 (+12)
중위 순회 (In-order Traverse) : Left -> Root -> Right 순서 방문 (1+2)
후위 순회 (Post-order Traverse) : Left -> Right -> Root 순서 방문 (12+)
단계 순회 (Level-Order Traverse) : Level 순서로 왼쪽에서 오른쪽 노드로 방문 (≑ BFS)
탐색 알고리즘 (Seaching)
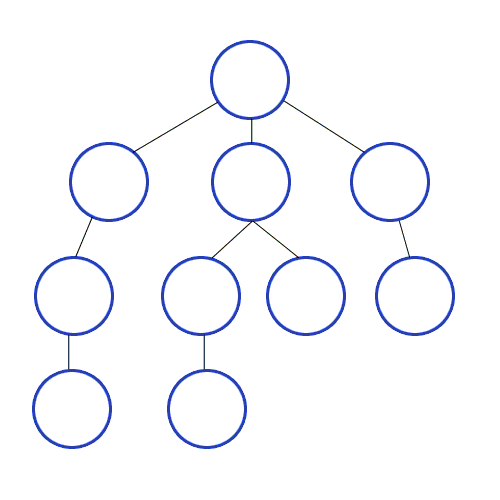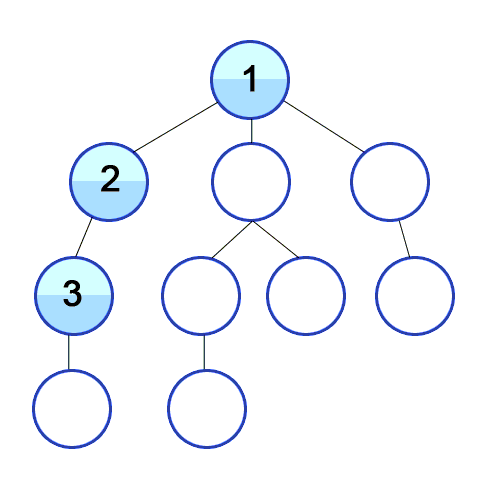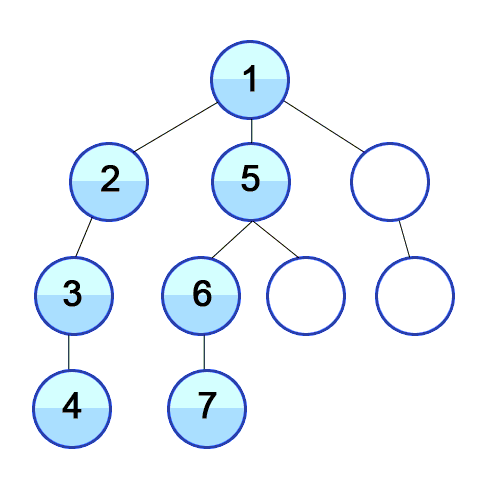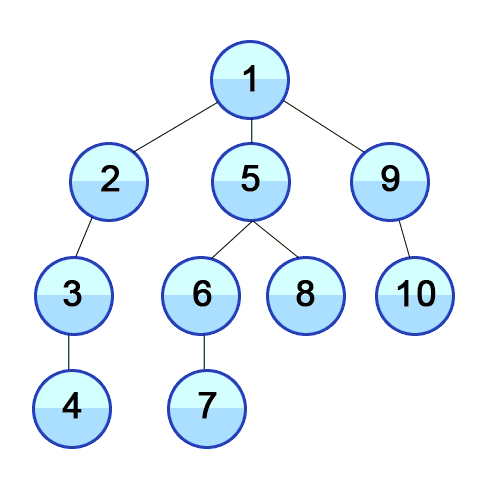
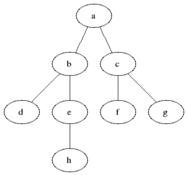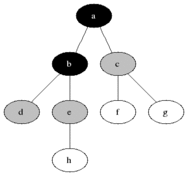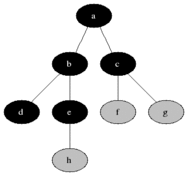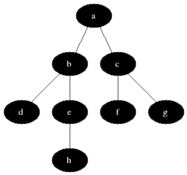
DFS / BFS 깊이 우선 탐색 (Death-First-Search, DFS) : 이진트리에서 조건에 맞는 자식노드의 Leaf Node까지 방문 후 Root로 돌아와 반복하는 탐색
너비 우선 탐색 (Breath-First-Search, BFS) : Level에 순서로 왼쪽부터 오른쪽 노드로 전체 탐색
이진 트리와 이중 연결리스트의 차이점
- 내부 구현은 동일하다, 하지만 트리의 순회 방식에 따라 이중 연결리스트 보다 빠른 탐색이 가능하다.
Wikipedia
Interview_Question_github
raywenderlich.com728x90'Archive > CS & App' 카테고리의 다른 글
[자료구조] Tree - AVL Tree (0) 2021.05.06 [자료구조] Tree - Binary Search Tree (0) 2021.05.06 [자료구조] Tree - 기초개념 (0) 2021.04.30 [자료구조] Hash Table (0) 2021.02.11 [자료구조] Linked List (0) 2021.02.11